Hizmetlerimiz

Modelleme Nedir?

Fiziksel bir sistemi, örneğin endüstriyel bir tesisi veya bir işletme sistemini deneme yanılma yoluyla incelemek, bozup tekrar tasarlamak oldukça maliyetli ve uzun bir süreç olurdu. Bunun yerine sistemin davranışlarını temsil eden denklemlerden oluşan matematiksel bir eşdeğer model üzerinde hesap yapmak işimizi oldukça kolaylaştırır.

Örneğin; Hızı saatte 90 km olan bir otobüsün 3 saat sonra nerede olacağını tahmin etmek için otobüse binip 3 saat gitmemiz gerekmez. Newton’un hareket yasasına göre alacağımız yolun matematiksel formülü Yol = Hız x Zaman ’dır. Otobüsün davranışını doğrusal ve zamanla değişmiyor kabul edersek (hız kesmiyor, mola vermiyor ... gibi) bu matematiksel modeli çözerek aracın 3 saat sonra yaklaşık olarak 270 km ilerde olduğu tahmininde bulunabiliriz.

Maliyet, Kâr ve Bütçe Simülasyonları

Çalışma ve iş sistemlerimizin işleyişini de benzer şekilde modelleyebiliriz. Matematiksel yöntemlerle kuracağımız modellerle, sadece parametreleri değiştirerek sonucu kolayca görebiliriz. Değişik senaryolar deneyebilir ve simülasyonlar yapabiliriz. Örneğin; değişik talep ve üretim seviyelerinde maliyet, kâr ve bütçe simülasyonları yapabilir, farklı senaryolara göre şirketin kârlılığını değerlendirebiliriz. Excel esnekliğinde, sadece birkaç parametre değiştirerek sonuçları süratle görüp, vereceğimiz kararlarda kullanabiliriz.

Optimizasyon

Sistemi yeterince temsil edecek bir model oluşturduktan sonra, sistem hakkında analizler yapabiliriz. İstenilen bir amaca bizi en çok yaklaştıracak, optimum veya en iyi çözümleri optimizasyon teknikleri ile bulabiliriz. Modelleme ve optimizasyon birçok işletme ve ekonomi sorunlarında, özel veya kamu sektöründe kullanılmaktadır. Nakliyat, enerji üretimi ve dağıtımı, telekomünikasyon, sınai üretim gibi teknik işletmecilik gerektiren alanlarda ve bankacılık gibi hizmet sektöründe bulunan birçok firmada optimizasyon sıkça kullanmaktadır. Planlama, zaman programlaması, iş ve işçi tahsis edilmesi, fireyi azaltma, finansal getiriyi maksimize etme gibi birçok sorun optimizasyon ile çözülebilir.

Optimizasyonda en çok kullanılan modeller, doğrusal (lineer) ve doğrusal olmayan (non-lineer) programlama dediğimiz matematiksel modellerdir. Excel Çözücü eklentisi (Solver), gerek doğrusal modellerin, gerekse doğrusal olmayan çoğu modellerin çözümünde kullanılmak için geliştirilmiştir.

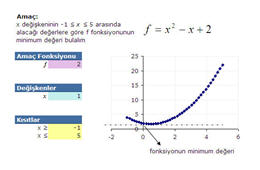
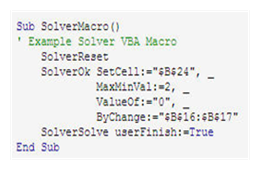
Örnek Problemler

Problem 1

Bir gemi şirketi gelecek dört mevsimde kaç adet yelkenli üreteceğine karar verecektir. Talep sırasıyla 40, 60, 75 ve 25 yelkenlidir. Şirket tüm talepleri zamanında karşılamalıdır. Başlangıçta şirket'in envanterinde 10 yelkenli vardır. Normal mesai ile bir mevsimde 40 yelkenli üretebilen şirket yelkenli başına $400 işçilik maliyetine maruz kalmaktadır. Fazla mesai ile yapılan her ek yelkenli için ise işçilik maliyeti $450'dır. Herhangi bir mevsimde yapılan yelkenli ya talebi karşılamak için kullanılıp satılır ya da envantere konulur. Bir yelkenlinin bir mevsim envanterde tutulması durumunda ise $20 envanter taşıma maliyeti oluşmaktadır. Sonuç olarak bu şirket her mevsimde ne kadar üretim yapmalıdır?

Problem 2

ABC şirketi, yüksek gelirli müşterileri için otomobil ve jeep üretmektedir. Televizyondaki tiyatro oyunlarına ve futbol maçlarına bir dakikalık spot reklamlar vererek satışlarını arttırmayı hedeflemektedir. Tiyatro oyununa verilen reklamın maliyeti $50bin'dir ve hedef kitledeki 7 milyon kadın ve 2 milyon erkek tarafından seyredilebilir. Futbol maçına verilen reklamın maliyeti ise $100bin'dir ve hedef kitledeki 2 milyon kadın ve 12 milyon erkek tarafından seyredilebilir. ABC şirketi yüksek gelirli 28 milyon kadın ve 24 milyon erkeğe en az maliyetle nasıl ulaşır?